



僕が出会った問題は、あまりにもクセの強い目的関数なので、コンピュータで、と言うことになる。そのために急遽、最適化問題を研究することになった。いやらしい関数で、僕の知っていた普通の方法では収束しない。つまり求まらない。
そうこうしている間に Nelder-Mead Method が良いらしいことがわかった。
幸い numpy によるコードが誰かが公表していた[2]。
まだ未完成な部分があるが、しかし、そのレベルで試してみると、この方法はなかなか優秀である。この手の問題の現在のスタンダードだと言われる理由がわかる。どうしてこんなにうまく行くの? との理由はまだよくわからない部分があるらしい。
とやかく調べて行くうちに、その改良版の論文が見つかった[1]。次元が高くなると Nelder-Mead Method が遅くなる原因を明らかにし、対策を示したのがこの論文である。著者らは、これを Adaptive Nelder-Mead Method と呼んでいる。そこで提案されたアルゴリズムを numpy で実装することにした。実装するに当たって nykergoto 氏のコードを利用させてもらった。何しろ彼のコードはよくできている。そこで可能な限り彼のコードとコメントを残すことにした。ツールとしては、関数として実装する必要があるので、その部分は追加した。それから元のコードには少し気に入らない部分(分かり難い場合分け)があったので修正した。それから、もちろん、"Adaptive" となるようにコードを追加した。
完成したものを試してみると、確かに素晴らしい。
download nmm.py -- 本体 (ver.1.1b)
download nmm_t.py -- 使い方のサンプル (ver.1.0)
download nmm_t2.py -- 使い方のサンプル (ver.1.1)
なお nmm.py の中の関数
snmsearch(objective, x0, err=1e-5,**k)
anmsearch(objective, x0, err=1e-5,**k)
機会があれば、ちゃんとした解説を加えたい。(解説を書きました)
十分にテストを行ったつもりであるが、まだ問題があれば知らせてもらえれば幸いです。
他にソースコードがどこかにあるか探したが、見つけるのが難しい。
見つかった唯一のソースコードは、統計ソフト R 用のもので[3]、Python によるコードは見つからない。
ここに公開したコードは、出典が添えられておれば自由に使ってよろし。もちろん責任は負わない。
引数の与え方に柔軟性を持たせ、初期単体として任意の形を許した。
旧版とは上位互換性あり。コードサンプルを追加した。
1次元の場合のバグを修正した。コメントを追加した。
過剰な警告を出さないようにした
バグの修正とコードの追加
Nelder-Mead Method は概して良く働くのであるが、ちゃんとローカルミニマムが求まる保証がない。
Adaptive Nelder-Mead Method についても同様である。
保証がないから使えないかと言えば、そうではない。保証がある関数の条件がはっきりしていないのが問題である。
Gao[1]は "uniformly convex" の条件のもとで収束性を論じている。しかしこの条件は実際のニーズからすればあまりにも強い。そして Gao が扱っているテスト関数の殆どは "convex" の条件すら満たしていない。
つまり Nelder-Mead Method はなぜこんなにうまく働くのは良くわかっていない、適用可能な関数の条件が良くわからないまま使われていると言ってよい。
筆者が扱っている問題(非常に癖の強い関数である)では、あきらかにローカルミニマムでない点を出している。そこで対策を立てた方が良いと考えた。求まった点 \(x\) がローカルミニマムであれば、\(x\) を囲むシンプレックスの頂点を \(x_1,x_2,...,x_m\) として
\begin{equation}
f(x) \le \min(f(x_1),f(x_2),...,f(x_m) \label{eq:1}
\end{equation}
の条件が成り立つべしと考えるのは自然である。そこで、これが成立していない時には警告を出すことにした。その場合次のようなメッセージを出す。
# Failed. not a local minimum: 8.29328101784887e-09 1.2983610054792913e-09
条件は過剰になることもある。しばしば関数の持つ丸め誤差が条件式(\ref{eq:1})を破る。
従って警告を無視して構わないか否かの判断は利用者に任せられている。
筆者が扱っている問題は、右辺がわずかに小さいのであるが、無視できないような問題である。
そのような微妙な問題は Nelder-Mead Method では扱えないことになる。
[1] Fuchang Gao · Lixing Han: "Implementing the Nelder-Mead simplex algorithm with adaptive parameters"
(Computational Optimization and Applications · May 2012)
https://www.researchgate.net/publication/225691623_Implementing_the_Nelder-Mead_simplex_algorithm_with_adaptive_parameters
[2] nykergoto: 『Nelder Mead Method を python で実装』
https://nykergoto.hatenablog.jp/entry/2019/11/06/Nelder_Mead_Method_%E3%82%92_python_%E3%81%A7%E5%AE%9F%E8%A3%85
[3] anms: Adaptive Nelder-Mead Minimization
https://rdrr.io/rforge/pracma/man/anms.html
2019-11-06
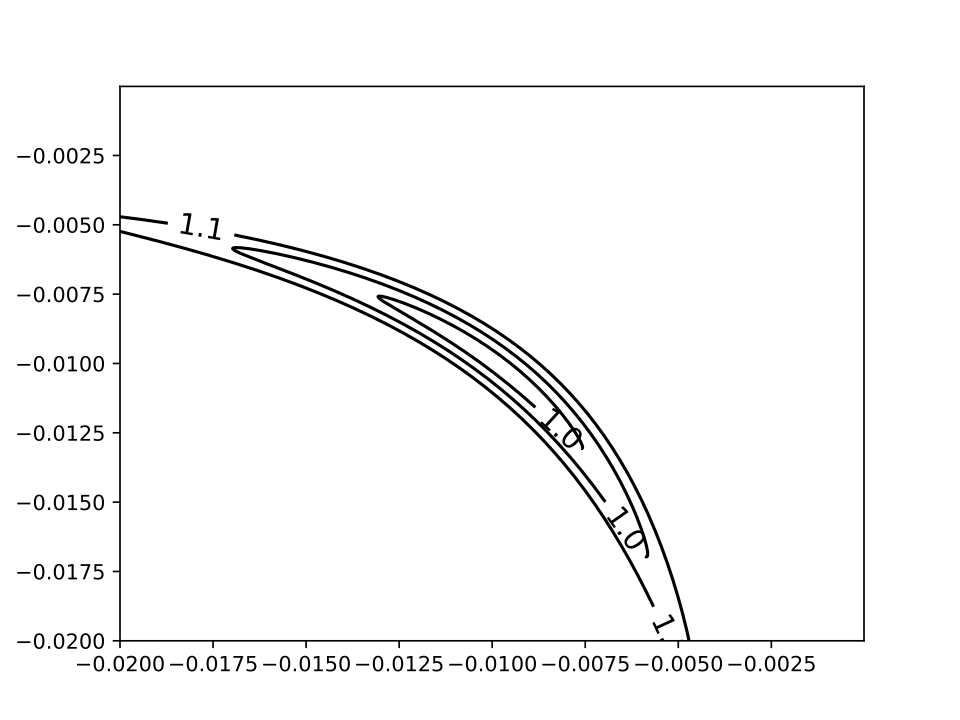
More[1] には、"Powell badly scaled function" が紹介されている。
この関数は次のように定義される。
# Powell badly scaled function # ref: More def powell(t): x1,x2 = t return (10**4*x1*x2 - 1)**2 + (exp(-x1)+exp(-x2) - 1.0001)**2
More によると、最小解は
f = 0 at (x1,x2)=(1.098e-5, 9.106)
(x1,x2)=(-0.00994809, -0.00994809)
[1] JORGE J. MORE, BURTON S. GARBOW, and KENNETH E. HILLSTROM
"Testing Unconstrained Optimization Software"
https://www.caam.rice.edu/~yzhang/caam454/nls/MGH.pdf
(ACM Transactions on Mathematical Software, Vol.7, No.1, 1981)
Nelder-Mead 法に関する記事を書きました。
数学の話なので、全部読むのは大変ですが...
Nelder-Mead 法にあまり関心がなくても凸解析の解説は役に立つのではないでしょうか?
有澤健治: 『Nelder-Mead 法の数学的基礎』download (改定版)
Abstract より引用
Mathematical foundation of Nelder-Mead simplex method is investigated under the objective function of continuous strictly quasiconvex function with bounded level set. It is shown that the diameters of simplex series converge to 0 if the number of consecutive reflections is always finite.
多くの新しい証明を含みます。でも証明は神経を擦り減らす。歳をとると辛い!
誤りが見つかりましたら、連絡して頂ければ助かります。
改定版(nmm3b.pdf): 旧版(nmm3.pdf)からの主な修正は、定理9,10の証明を丁寧にしたこと。