メモリの上での2進数の扱い

従って、もしも2バイトのメモリに整数を格納する場合に負の整数を扱う必要がないなら、ここには 0 から 65535 までの整数が格納可能である。

さて、最後の数に 1 を加えるとどのようになるか? 普通の2進数の計算では

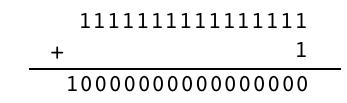
となるが、今の場合には(16ビットしか使えないので)この数は記憶できない! (これを桁溢れと言う。)　この場合の処理としては2つの考え方がある。

1. エラーとして処理する考え方
   
2. エラーとして処理しないで計算を続行する考え方
   

第２の考え方では溢れた 1 を捨てて、

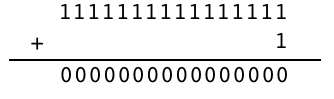
とみなすのである。

注意: 第2の考え方は特殊な考え方ではない。同様な考え方は身近に多く見られる。例えば自動車の走行距離を表示するデジタルカウンタは 999999 のあと、000000 に戻る。

自動車の走行メーター

計算機での整数計算は普通は第2の考え方に立つ。理由は、このように考えることによって負の整数を自然に扱えるからである。

■ 負の整数の扱い

第2の考え方に立つと他の整数は次のように考えることができる。

負の数、例えば -1 は 1 を加えると 0 になる数である。すなわち、

	-1 + 1 = 0

従って

-1 = 1111111111111111(2)

同様に

-2 = 1111111111111110(2)

-3 = 1111111111111101(2)

...

2バイトで扱える数の個数 65536 の半分を負の数とみなす場合には左端の1ビットの値が 0 の場合に非負整数(負でない整数)、1の場合に負の整数と考える。すると負の数を考慮に入れた対応関係は次のようになる。

■ 計算機の不思議な数の世界

2バイトのメモリでは 65536 は 0 とみなされるので、数字が書かれたテープを次の図のように 65536 を 0 と重ね合わせて張り合わせた円環と似ている。65535 は 0 の手前の数字なので −1 とみなすことができる。

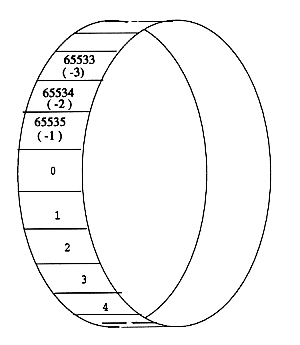
図1

問題3

4ビットのメモリを使って負の整数を含む整数を扱う場合にはメモリの状態に応じてどの数が割り当てられるか?

内部状態	10進数
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	?
0111	?
1000	?
1001	?
1010	?
1011	?
1100	?
1101	?
1110	?
1111	?

問題4.

• 1バイトのメモリは何通りのデータを記憶できるか?
  
• 1バイトのメモリが非負整数を扱う場合には 0 からいくつまでの数を扱えるか?
  
• 1バイトのメモリが負の数を含む整数を扱う場合には、表2に習って、扱える数の範囲を明らかにせよ。